Lect03. Divide and Conquer
Quick sort
prof.이도훈
school of computer science & engineering
pusan national university
개인의 학습 목적의 수업 내용의 정리입니다.
*** 이하는 개인적인 추가내용이므로 혹여, 잘못된 점이 있다면 댓글로 남겨주세요.
1. Quick sort
- C.A.R. Hoare(찰스 앤터니 리처드 호어, 1962 영국)에 의해 발명
- 기본 개념은 정해진 pivot, 기준 값과 비교해서 작으면 왼쪽 크면 오른쪽에 두는 방법
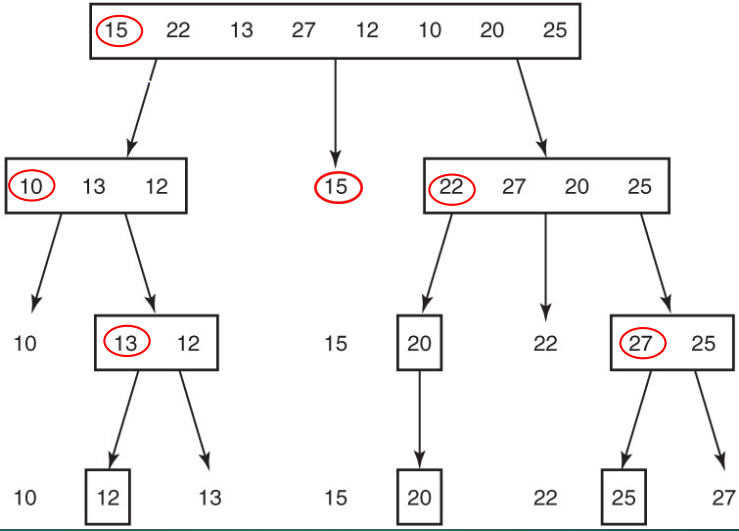
- 빨간 동그라미가 pivot. 배열의 각 값을 pivot과 비교, 정렬
2. 전체 알고리즘
- 문제 : 정렬되지 않은 n 개의 키를 정렬해라
- input : 양의 정수 n, 배열 S[1..n]
- output : 정렬된 배열 S[1..n]
- 알고리즘
void quicksort (index low, index high) {
index pivotpoint;
if(high > low){
partition(low,high,pivotpoint);
quicksort(low,pivotpoint-1);
quicksort(pivotpoint+1,high);
}
}- 여기서 low는 배열의 처음, high는 배열의 마지막을 의미. 즉 인덱스 값의 작고 큼을 뜻함.
3. partition 알고리즘
- 문제 : 배열 S를 분할
- input: low,high 가 될 지표 두 개 / 서브 배열 S[low..high]
- output: pivotpoint(얘는 서브 배열의 인덱스 값을 low 부터 high까지 가르킬 포인터)
- 알고리즘
void partition (index low, high, index& pivotpoint) {
index i,j;
keytype pivotitem;
pivotitem = S[low]; // 배열의 첫번째 아이템을 가르킴
j = low;
for(i = low + 1; i<=high; i++){
if(S[i]<pivotitem){
j++;
exchage S[i] and S[j];
}
pivotpoint = j;
exchange S[low] and S[pivotpoint]; // pivotitem을 pivotpoint에 대입
}
}
4. 분석
- 오퍼레이션 : S[i]와 pivotitem의 비교
- input size : n=high-low+1 >> 서브 배열의 원소 개수
- 최선의 시간복잡도
- 총 배열의 원소 개수가 2^k개를 가지는 경우
- 순환 호출의 깊이 * 각 단계에서의 비교 연산
- 각 단계에서 거의 리스트 대부분을 비교해야하므로 평균 n번 비교
- 순환 호출은 2^k를 2개씩 나누어 도달하므로 log2번
- 따라서 대략 nlogn번의 연산필요
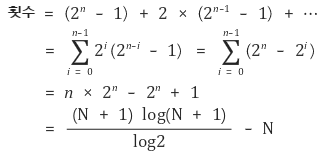
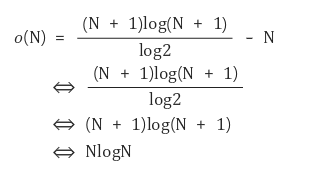
- 최악의 시간복잡도
- 오퍼레이션 : S[i]와 partition 안의 pivotitem과 비교
- input size : n >> 원 배열 S의 원소 개수
- 분석 : 최악의 경우 = 아이템들이 정렬되어 있는경우
- T(n) = T(0) + T(n-1) + n+1 >> 왼쪽 서브 배열 정렬 시간 + 오른쪽 서브 배열 정렬 시간 + 나누는 시간
- T(n) = T(n-1) + n-1 for n>0, T(0) = 0
- T(n) = T(n-1) + n-1 >> T(n) = 1 + 2 + 3 + ... + (n-1) = n(n-1)/2


5. 정리
- 시간복잡도가 다른 O(nlogn)을 가지는 정렬 알고리즘보다 빠르다.
- 불필요한 데이터의 이동을 최소화하고 먼 거리의 데이터를 교환, 한번 결정된 피벗들이 추후 연산에서 제외되기 때문이다.
- 추가 메모리 공간을 필요로하지않는다.(O(logn)만큼의 메모리만 사용)
- 단, 이미 정렬되어 있는 데이터를 대상으로는 불균형한 분할 때문에 수행시간이 더 많이 걸린다.
- 피벗을 잘 선택하는 것이 성능에 영향을 미친다.
6. master theorem : 마스터 정리_재귀 알고리즘의 점근적 행동
- 간단하게 시간복잡도를 구할 수 있는 정리
- 알고리즘을 분석할때, 점근적 행동에만 집중할 것
- 재귀 알고리즘도 마찬가지
- 알고리즘의 비용과 관련된 반복 관계를 정확히 해결하는 것보다는 점근적 특성을 보는 것으로 충분
- 그것을 하기 위한 도구_master theorem.
7. 3가지 공식
- T(n) = a * T(n/b) + f(n) 모양의 점화식은 마스터 정리에 의해 바로 결과를 알 수 있다.
- T(1) = 1, a≥1, b≥2, c>0
- f(n) = Θ(n^d), d≥0
- 위의 조건들을 만족할 때, T(n)은 3가지 공식으로 시간복잡도를 적용 할 수 있다.

>> g(n)이 더 무거우면 g(n)이 수행시간을 결정, f(n)이 더 무거우면 f(n)이 수행시간을 결정, 둘이 같다면 g(n)*logn을 한 값이 수행시간
8. 마스터 이론의 예외(사용 할 수 없을 때)
- T(n)이 단조함수가 아닌경우 ex)sin(x)
- f(n)이 다항식이 아닌경우 ex)T(n) = 2T(n/2) + 2^n
- b가 상수로 표현되지 않는 경우 ex)T(n) = T(√2)
- 반복 방정식을 해결 하지 않음.
9. 행렬 곱셈
- 기본 행렬 곱셈 알고리즘
- 문제 : n*n 행렬 두개 곱하기
- input : n*n 행렬 A, B
- output : 새로운 행렬 C
- 알고리즘
void matrixmult (int n, const number A[][], const number B[][], number C[][]) {
index i, j, k;
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++) {
C[i][j] = 0;
for (k = 1; k <= n; k++)
C[i][j] = C[i][j] + A[i][k] * B[k][j];
}
}- 시간 복잡도 1:
- 기본 오퍼레이션 : 루프에 대한 가장 안쪽의 곱셈 명령
- input size : n, 행과 열의 개수
- 모든 케이스의 시간복잡도 분석 : 곱셈의 총 횟수 T(n) = n * n * n = n^3 ∈ Θ(n^3)
- 시간 복잡도 2:
- 기본 오퍼레이션 : 루프에 대한 가장 안쪽의 덧셈 명령
- input size : n, 행과 열의 개수
- 모든 케이스의 시간복잡도 분석 : 덧셈의 총 횟수 T(n) = (n-1) * n * n = n^3 - n^2 ∈ Θ(n^3).
10. 슈트라센 알고리즘
- 기본적으로 n*n 행렬 두개를 곱하면 위에서 처럼 Θ(n^3)이 걸리지만, 슈트라센 알고리즘은 대략 Θ(n^2.807) 의 시간복잡도를 가진다. 단, 수치 안정성은 떨어진다고 평가받는다.
- n이 일반적인 크기로 작다면 기본 방법을 사용하자.
- C = AB 일때, A 와 B를 2^n * 2^n 형태로 모자라는 행과 열을 0으로 채워 만들어준다.
- 그 후 세 행렬을 같은 크기의 정사각형 행렬 4개로 나눈다.
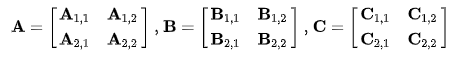
- 그러면 다음과 같은 식이 성립하며, 이 과정까지는 아직 연산의 개수가 줄지않았다.

- 다음과 같은 행렬을 정의한다.

- 이 Mk 행렬들은 Ci,j 행렬을 표현하는 데 쓰이는데, 이 행렬들을 계산하는 데는 일곱 번의 곱셈(각 변수마다 한 번씩)과 10번의 덧셈이 필요하다. 이제 Ci,j 행렬은 다음과 같이 표현할 수 있다.
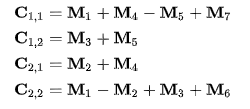
- 이 과정에서는 곱셈이 사용되지 않기 때문에, 전체 곱셈을 7 번의 곱셈과 18번의 덧셈으로 처리할 수 있다.
- 기존의 방식은 곱셈 8번, 덧셈 4번이 필요하다.
- 큰 행렬에 대해서는 행렬의 곱셈이 덧셈보다 더 많은 시간을 필요로 하기 때문에 덧셈을 더 하는 대신 곱셈을 덜 하는 것이 전체적으로 더 효율적이다.
- 이 과정을 재귀적으로 반복할 경우 총 T(n) = 7*T(n/2) - 18*((n/2)^2) 번의 연산
- lg7 = 2.807...
- 시간복잡도는 Θ(n^2.807)
- 알고리즘
void strassen (int n, n*n_matrix A, n*n_matrix B, n*n_matrix& C) {
if (n <= threshold )
compute C = A x B using the standard algorithm ;
else {
partition A into four submatrices A11, A12, A21, A22 ;
partition B into four submatrices B11, B12, B21, B22 ;
compute C = A x B using Strassen’s method ;
// example recursive call: strassen(n/2, A11+A12, B11+B22,M1)
}
}
11. 토론
- 시간 복잡도가 Θ(n^2)인 알고리즘은 x
- 하지만 그런 알고리즘이 불가능하다는 것을 밝히지도 못했다.
12. 분할정복을 쓰지 않는 경우
- n크기의 인스턴스가 거의 n과 비슷한 크기의 인스턴스들로 둘 이상 나누어질때 >> 시간복잡도가 지수 시간을 가짐
- n 크기의 인스턴스가 n/c 크기의 거의 n개의 인스턴스로 나뉠때. 이땐 c는 상수.
'CS > 알고리즘 & 자료구조' 카테고리의 다른 글
| computer algorithm_03(1) (0) | 2021.04.17 |
|---|---|
| computer algorithm_01(1) (0) | 2021.04.16 |