computer algorithm_03(1)

Lect03. Divide and Conquer

merge sort

 

prof.이도훈

school of computer science & engineering

pusan national university

개인의 학습 목적의 수업 내용의 정리입니다.

*** 이하는 개인적인 추가내용이므로 혹여, 잘못된 점이 있다면 댓글로 남겨주세요.

 

참고 :

wonillism.tistory.com/17

[Algorithm - Theory]반복문과 재귀함수의 차이

 

1. 분할정복을 이용한 이진탐색

• 개념

Figure 2.1 : The steps down by a human when searching with Binary Search. (Note: x = 18)

• 접근 >> top-down
• 1 ) 문제의 인스턴스(input size)를 한개 혹은 더 작은 인스턴스들로 나눈다.
• 2 ) 작아진 인스턴스를 각각 해결한다. 나뉜 배열이 충분히 작아질 때 까지 재귀를 사용.
• 3 ) 소규모 인스턴스의 솔루션을 결합하여 원래 인스턴스의 솔루션을 가져옴.

 

2. 이진탐색 : 재귀 알고리즘

• 문제 : x가 n 개의 원소를 가진 정렬된 배열 s에 존재하는지 정의하라
• input : 양의 정수 n, 비내림차순으로 정렬된 s(1 ~ n), 키로 사용될 a
• outpu : s안의 x의 위치
• method : 
  • if x == array[middle], then 'find' else :
  • divde: 배열을 분할, array[middle]의 값을 체크. if value >x then select left of array, else select right of array
  • concuer : find x를 해라, 선택된 절반의 배열에서.
  • combine: 필요하다면

 

3. 이진탐색 : 재귀 알고리즘

index location (index low, idnex high) {
	index mid;
    
    if(low > high)
    	return 0; 	//fail
    else {
    	mid = (low + high) /2
        if (x==s[mid])
    return mid;		//find
    	else if (x < s[mid])
    return location(low, mid-1); //select left side
    	else
    return location(mid+1, high); //select right side
    }
}
...
locationout = location(1, n);
...

 

4. 토론(재귀:recursion vs 반복:iteration)

• 이진탐색은 인스턴스가 하나의 작은 인스턴스로만 분할되어 출력의 조합이 없어 분할 정보 알고리즘의 가장 간단한 종류. 최종 솔루션은 작은 인스턴스에 대한 솔루션.
• 이진탐색의 재귀 버전은 재귀 호출(꼬리 재귀:tail-recursion) 후 작업이 수행되지 않음을 이용. 반복 버전을 생성하는 것은 간단.
• 반복 알고리즘은 스택을 유지 할 필요가 x. 재귀 알고리즘보다 빠르게 실행되기 때문에 성능 측면에서는 반복을 사용하는 것이 좋다. 다만, hw의 품질 향상과 협업의 증가로 코드의 가독성 등을 생각한다면 재귀함수를 사용한다.

*** 재귀 알고리즘이 느린 이유 : 함수 호출 시 함수가 호출된 위치를 주소 값에 저장해야함. 함수가 재귀적으로 호출 될 경우 함수 안에서 함수가 호출, 차례로 리턴 -> 호출횟수가 늘어나면 리턴될 곳의 주소값을 저장한 스택이 넘치거나 느려짐. 즉 함수가 호출된 위치를 저장하기 때문에 발생.

*** 꼬리 재귀 : tail-recursion : 재귀 알고리즘의 느린 이유인 리턴 한 위치, 함수가 호출된 위치를 기억하기 때문. 일반적으로 재귀함수의 경우 리턴되는 함수 값을 받아 다시 연산을 반복. 함수가 호출된 위치로 돌아갔을 때, 실행될 작업이 없다면, 즉 재귀의 형태를 한 반복문으로 바꿔주는 것. 컴파일러가 하는 일이므로 지원이 안될수도.

 

5. 최악의 시간 복잡도

• 기본 연산 : x와 s[mid]의 비교
• input size : n, 배열의 아이템 수. (= high - low + 1) >> 여기서 high, low는 인덱스 값

 

6. 최악의 시간복잡도 계산

• case 1 : n이 2^n 일때
• w(n) = w(n/2) + 1 , n > 1 & n = 2^k(k≥1)
• w(1) = 1
• 1은 상수

w(1) = 1

w(2^1) = w(1) + 1 = 2

w(2^2) = w(2) + 1 = 3

w(2^3) = w(4) + 1 = 4

...

w(2^k) = k + 1

∴ w(n) = lgn+1

 

• case 2 : 절반으로 나눈 배열의 크기가 n/2 이하의 가장 큰 정수 일때(in general)
• n 이 인덱스의 중간값, mid=(1+n)/2 이하 가장 큰 정수 라면, 서브 배열의 크기는 다음과 같다.

• 즉, w(n) = 1 + w(n/2)이하 가장 큰 정수

 

7. mergesort

• two-way merging을 사용. 정렬된 두 배열을 하나의 배열에 합친다. 합병 과정을 반복 적용하면서 정렬된 배열을 얻는다.
• 결국 하위 배열의 크기는 1이되고 크기 1의 배열은 정렬됨.
• 정렬된 크기 1의 하위 배열들을 비교하며 다시 하나의 큰 배열로 합병하는 것.

 

8. 병합 정렬의 단계

• divde : 처음의 정렬되지 않은 배열을 두개의 서브 배열로 각각 n/2의 크기로 나눔
• sort : 각 서브 배열을 충분히 작은 크기까지 나누어 비교, 정렬
• combine : 정렬된 크기 1의 서브 배열을 상위 배열로 병합함.

 

9. 예시

• 문제 : 비내림차순의 n 개의 키를 가진 수열을 정렬하는 것.
• input : 양의 정수 n, 키의 배열 s[1..n]
• output : 정렬된 배열 s[1..n]
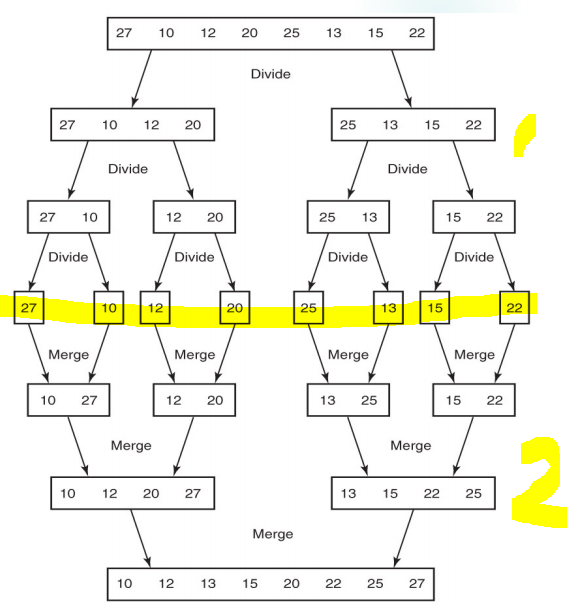
• ex : s[27, 10, 12, 20, 25, 13, 15, 22]

 

10. 풀이

void mergesort (int n, keytype S[]) {
	const int h = n/2, m = n - h;
    keytype U[1...h], V[1...m];
    
    if(n>1){
    	copy S[1] through S[h] to U[1] throught U[h];
        copy S[h+1] through S[n] to V[1] throught V[m];
        mergesort(h,U);
        mergesort(m,V);
        merge(h,m,U,V,S);
    }
}

맨 처음 입력받은 배열 S를 작은 U, V 배열로 나눔.

mergesort라는 함수 recursive한 구조로시행. 계속해서 n/2의 크기로 배열의 크기가 1이 될 때 까지 divide.

그림의 1부분

 

void merge(int h, int m, const keytype U[], const keytype V[], const keytype S[]) {
	index i, j, k;
    i=1; j=1; k=1;
    while (i<=h && j<=m){
    	if(U[i] < V[j]){
        	S[k] = U[i];
            i++;
        }
        else {
        	S[k] = v[j];
            j++
        }
        k++;
    }
    if (i>h)
    	copy V[j] through V[m] to S[k] through S[h+m];
    else
    	copy U[i] through U[h] to S[k] through S[h+m];    	
}

 

크기가 1인 배열들을 하나의 정렬된 배열에 병합하는 과정

input으로 양의 정수 h,m을 받고 위의 mergesort에서 정렬된 하위 배열 U[1..h], V[1..m]을 받음

output으로 최종 병합정렬된 S[1..h+m]을 산출

그림의 2 부분

Figure 2.2: The steps done by a human when sorting with Mergesort

 

11. 시간복잡도

• 병합 정렬의 시간 복잡도는 O(nlogn). 최악의 시간 복잡도 역시 O(nlogn).
• 순환 호출의 깊이, 즉 divide 되는 수는 계속해서 절반으로 나누어가기 때문에 8(2^3)개를 1이 될때 까지 나누면 총 3단계를 거친다. 4개(2^2)은 2번. 이것을 일반화하면 n = 2^k일 때, k = 밑이 2인 logn.
• 나뉜 배열을 다시 합병 단계를 거치기 위해서는 최악의 경우 n 번의 비교가 필요하다.
• 따라서 모든 깊이에 대해 합병을 진행하기 때문에 시간복잡도는 O(n*logn)이 된다.